Project Euler (pronounced "Oiler") provides a number (~182) of challenging math/programming problems... which is a fantastic environment to play with F#!
I've only completed 6% of the questions but I've already learnt a lot. (F# is huge)
If you have some free time (or get bored during your compiles), I'd definitely recommend having a go - in your own language of choice of course!
Showing posts with label maths. Show all posts
Showing posts with label maths. Show all posts
Wednesday, February 20, 2008
Tuesday, January 15, 2008
Deriving Miss Daisy
As I've mentioned previously, I'm slowly reading through SICP - it's an amazing book and reading it has been a humbling experience.
'Geeking' Out
I completely geeked out reading one example on functional derivatives. (Take a math expression as a parameter and return the derivative as an expression)
It's in the first chapter, and they use this to implement Newton's Method -> to then implement a Sqrt function!
Approximate Derivative
After I picked my brain off the floor, I decided to have a crack at implementing derivatives in C# using lambda expressions:
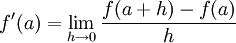
Using the formula of a derivative (above), we can simply code an approximate derivative (below):
Symbolic Derivation
Easy huh! So for fun I decided to use linq expression trees to derive algebraically.
It's easy to get an expression tree in C# - simply use the Expression<> type.
I parse the expression tree using Matt Warren's ExpressionVisitor class - and using the basic rules of Derivation (Constant, Product and Quotient rules) we get:
Wrapping it up
To quickly finish this long blog post, here's the usage code:
And there it is! Useful? maybe not. Fun? Definitely!
'Geeking' Out
I completely geeked out reading one example on functional derivatives. (Take a math expression as a parameter and return the derivative as an expression)
It's in the first chapter, and they use this to implement Newton's Method -> to then implement a Sqrt function!
Approximate Derivative
After I picked my brain off the floor, I decided to have a crack at implementing derivatives in C# using lambda expressions:
Using the formula of a derivative (above), we can simply code an approximate derivative (below):
Func<double, double> Approximate(Func<double, double> f)
{
var h = 0.0001;
return a => ((f(a + h) - f(a)) / h);
}
Symbolic Derivation
Easy huh! So for fun I decided to use linq expression trees to derive algebraically.
It's easy to get an expression tree in C# - simply use the Expression<> type.
Func<double, double> Derive(Expression<Func<double, double>> e)
{
var lambda = new Derivative().Eval(e) as LambdaExpression;
return (Func<double, double>) lambda.Compile();
}
I parse the expression tree using Matt Warren's ExpressionVisitor class - and using the basic rules of Derivation (Constant, Product and Quotient rules) we get:
class Derivative : ExpressionVisitor
{
public Expression Eval(Expression exp)
{
return this.Visit(Evaluator.PartialEval(exp));
}
protected override Expression VisitBinary(BinaryExpression b)
{
// Product Rule: (fg)' = f'g + fg'
if (b.NodeType == ExpressionType.Multiply)
{
return Expression.Add(
Expression.Multiply(Eval(b.Left), b.Right),
Expression.Multiply(b.Left, Eval(b.Right)));
}
// Quotient Rule: (f/g)' = (f'g - fg') / (g*g)
if (b.NodeType == ExpressionType.Divide)
{
return Expression.Divide(
Expression.Subtract(
Expression.Multiply(Eval(b.Left), b.Right),
Expression.Multiply(b.Left, Eval(b.Right))),
Expression.Multiply(b.Right, b.Right));
}
return base.VisitBinary(b);
}
// Parameter Derivation: f(x)' = 1
protected override Expression VisitParameter(ParameterExpression p)
{
return Expression.Constant(1.0);
}
// Constant Rule f(a)' = 0
protected override Expression VisitConstant(ConstantExpression c)
{
return Expression.Constant(0.0);
}
}
Wrapping it up
To quickly finish this long blog post, here's the usage code:
// f(x * x * x)' = 3 * x * x
var approx = Approximate(x => x * x * x);
var derive = Derive(x => x * x * x);
var y1 = approx(1); // 3.0000300001109532
var y2 = derive(1); // 3.0
And there it is! Useful? maybe not. Fun? Definitely!
Monday, November 5, 2007
n! - let me count the ways
The other day I had an interesting discrete maths assignment question involving permutations - so I decided to codify it.
"How many ways can six people (Josh, Toby, CJ, Sam, Leo & Donna) sit, if Josh must sit to the left of Leo and to the right of Sam."
Now the astute reader will immediately recognize the answer to be 2 * (4! + 3!3!) = 120; but to be sure I wanted to double check this via C#. (I'm keen to redo this in F# too)
My solution was a quick hack, and is by no means "the best way" - but using linq it sure looks pretty.
This simple example shows why I'm a such fan of linq in C# - the pre-linq code for this certainly wouldn't be as eloquent.
Oh, and it also shows why I'm a fan of maths... it's much more efficient to just to calculate the factorials.
Update: Formatting code in a blog sure is a pain!
"How many ways can six people (Josh, Toby, CJ, Sam, Leo & Donna) sit, if Josh must sit to the left of Leo and to the right of Sam."
Now the astute reader will immediately recognize the answer to be 2 * (4! + 3!3!) = 120; but to be sure I wanted to double check this via C#. (I'm keen to redo this in F# too)
My solution was a quick hack, and is by no means "the best way" - but using linq it sure looks pretty.
class Program
{
static IEnumerable<List<string>> Permutate(IEnumerable<string> people,
IEnumerable<string> current)
{
// Get remaining people and recurse
foreach (var person in people.Where(x => current.Contains(x) == false))
foreach (var result in Permutate(people, current.Concat(new string[] { person })))
yield return result;
if (current.Count() == people.Count())
yield return current.ToList();
}
static void Main(string[] args)
{
string[] people = new string[] { "Josh", "Toby", "CJ", "Sam", "Leo", "Donna" };
var result = Permutate(people, new string[] { }).ToList();
// Josh sits to the left of Leo
var Josh_Leo = result.Where(r =>
r.FindIndex(x => x == "Josh") < r.FindIndex(x => x == "Leo"));
// Josh sits to the right of Sam
var Sam_Josh = Josh_Leo.Where(r =>
r.FindIndex(x => x == "Sam") < r.FindIndex(x => x == "Josh"));
var count = Sam_Josh.Count();
}
}
This simple example shows why I'm a such fan of linq in C# - the pre-linq code for this certainly wouldn't be as eloquent.
Oh, and it also shows why I'm a fan of maths... it's much more efficient to just to calculate the factorials.
Update: Formatting code in a blog sure is a pain!
Tuesday, October 2, 2007
I don't want to be a Maths Teacher
Before I started my maths degree I braced myself for the inevitable question "why maths?"
That's okay, maths isn't everyones favorite subject - but as it turns out the more popular question is "do you want to be a Maths teacher?"...
No!
Don't get me wrong, I have no problems with teaching, in fact it might be cool to be a lecturer one day... but it makes me sad that people think learning maths is only good for teaching maths.
It's like the definition of Recursion: see Recursion; a tragic cycle of futility; a perpetual motion machine that affects nothing and goes nowhere.
No!
I want to shout out from the roof tops - don't people realize that maths is the basis of all technology and human advancement?
Economically, math brings order to chaos. The steady job, the home (or mortgage), even food on the table and clothes on our backs - thank maths. Too melodramatic? Google the Great Depression sometime.
Math heals us when we are sick. Statistical drug trials determine what medicine works, mathematical models of the human body are used by doctors and physiotherapists to determine better techniques for recovery.
I won't even get started on computers or civil construction.
Above all, maths is eloquent, philosophical and beautiful. It changes your perceptions and makes you appreciate everyday life even more.
</rant>
That's okay, maths isn't everyones favorite subject - but as it turns out the more popular question is "do you want to be a Maths teacher?"...
No!
Don't get me wrong, I have no problems with teaching, in fact it might be cool to be a lecturer one day... but it makes me sad that people think learning maths is only good for teaching maths.
It's like the definition of Recursion: see Recursion; a tragic cycle of futility; a perpetual motion machine that affects nothing and goes nowhere.
No!
I want to shout out from the roof tops - don't people realize that maths is the basis of all technology and human advancement?
Economically, math brings order to chaos. The steady job, the home (or mortgage), even food on the table and clothes on our backs - thank maths. Too melodramatic? Google the Great Depression sometime.
Math heals us when we are sick. Statistical drug trials determine what medicine works, mathematical models of the human body are used by doctors and physiotherapists to determine better techniques for recovery.
I won't even get started on computers or civil construction.
Above all, maths is eloquent, philosophical and beautiful. It changes your perceptions and makes you appreciate everyday life even more.
</rant>
Subscribe to:
Posts (Atom)